Задача поиска

Более сложными, чем задачи линейного программирования, являются задачи выпуклого программирования. Прежде чем привести пример такой задачи, связанной с безопасностью жизнедеятельности, дадим некоторые определения из теории выпуклого анализа [39].

Определение 1. Множество Х из пространства Rn называется выпуклым, если из того, что две точки у и z принадлежат этому множеству, вытекает, что и весь отрезок {у,z}={хÎRn:х=lу+(1-l)z,  0

l1, соединяющий эти точки, также принадлежит этому множеству.

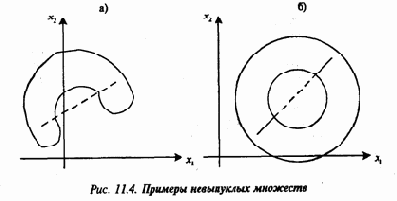
Очевидным примером выпуклых множеств является внутренность круга, шара, эллипсоида, куба. На рис. 11.4 а, б приведены примеры невыпуклых множеств на плоскости R2.

Определение 2. Функция f(x), определенная на выпуклом множестве xÌ Rn, называется выпуклой, если для любых двух точек у и z, принадлежащих X, и любого lÎx[0,1] (тогда отрезок [ly+(1-l)z], 0

l1, целиком принадлежит X) выполняется неравенство

,                  (11.9)

Замечание. Если неравенство (11.9) имеет противоположный знак, то функция f(x)

называется вогнутой.

Проще всего представить график выпуклой (или вогнутой) функции на плоскости (рис. 11.5).

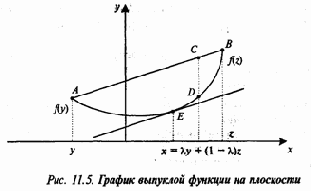
Правая часть неравенства (11.9) представляет собой отрезок АВ, соединяющий точки (y,f(y))=АиВ=(z,f(z)), причем каждая точка этого отрезка (на рисунке взята точка С) выше соответствующей точки графика (на рисунке точка D).

Если функция f(x) достаточно гладкая, то условия выпуклости (вогнутости) можно выразить через ее вторую производную.

Действительно, согласно теореме Лагранжа в некоторой точке Е (рис. 11.5) касательная к графику функции АВ лежит ниже этого графика. Уравнение этой касательной Y = f(x) + f'’(x)(x-x), следовательно, f(x)- f(x) – f’(x)(x-x)

0, откуда в силу формулы Тейлора

где 0<Q<1.

Деля последнее неравенство на (х-x)2 и далее переходя к пределу при х >

x, получаем, что

f”(x)

0.                  (11.10)

В силу произвольности точки x это неравенство справедливо на всем отрезке [у, z] и является условием выпуклости (в случае вогнутости справедливо обратное неравенство).
Для иллюстрации рассмотрим два простых примера.
Пример 1. f(x) =ex, xÎ
(-¥,+¥), f(“) = eх > 0, следовательно, показательная функция выпукла на всей оси.
Пример 2. f(x) = sin x, xÎ[0,2p], f”(x) = - sin x, следовательно, функция sin x вогнута на отрезке [0, ?] и выпукла на отрезке [?, 2 ?].
Прежде чем сформулировать задачу поиска, отметим, что оптимизационная задача
f(x)
> min, х Î
Р (f(x) > max, х Î Р),                  (11.11)
где в случае max целевая функция f (х) выпукла, в случае min – вогнута и Р –
полиэдр, называется задачей выпуклого программирования. Ясно, что задача линейного программирования является ее частным случаем.
Задача поиска. Объект, подлежащий обнаружению, находится в одном из п районов с вероятностями р1,..., рп соответственно. Для поиска объекта имеется общий ресурс времени Т (т. е. при t>T поиск считается нецелесообразным). Известно, что при поиске в i-м районе в течение времени ti, вероятность обнаружения объекта (при условии, что он там находится) выражается через функцию Бернулли 1-

, где ai>0 – заданное число (формула показывает, что за бесконечное время ti объект был бы найден). Требуется распределить по районам время наблюдения (поиска) так, чтобы максимизировать вероятность обнаружения объекта. Соответствующая задача оптимизации имеет вид
                    (11.12)
               (11.13)
              (11.14)
Из теории вероятностей хорошо известно, что
               (11.15)
Кроме того, очевидно, что задача g(x)>max эквивалентна задаче (-g(x))>
min; также очевидно, что условия (11.13) и (11.14) определяют определенный полиэдр Р (рис. 11.6). Следовательно, вводя целевую функцию  получаем следующую оптимизационную задачу:
, (11.16)
 где Р– полиэдр, заданный неравенствами (11.13) и (11.14).

Так как  причем ,   то  функция f(t) выпуклая и мы имеем задачу выпуклого программирования. Общие методы решения таких задач довольно сложны, однако в нашем конкретном случае можно предложить наглядное геометрическое решение.


Действительно, имеем <0. Значит, функция f(t) убывает по любому переменному ti, i = 1, 2,...,n,
и ее наименьшее значение достигается на гиперплоскости t1
+ t2 +…+ tn
= T (в случае двух переменных это прямая АВ на рис. 11.6). Однако в отличие от задач линейного программирования это наименьшее значение достигается необязательно в вершинах А, В и т.д., в чем можно убедиться, исследуя на АВ функцию f(t) в случае двух переменных. Тогда f(t1,t2)= Минимум этой функции может достигаться и внутри отрезка [0, T] в зависимости от соотношения параметров р1, р2,
?1, ?2, в чем можно убедиться непосредственным исследованием функции одного переменного (например, если  то минимум достигается в середине Е отрезка АВ).

Содержание раздела

---