Игровые модели
Часто возникают ситуации, в которых различные участники имеют не совпадающие между собой интересы. Математические модели и методы для исследования таких так называемых конфликтных ситуаций получили название теории игр [18].
Приведем простейшие понятия и результаты этой теории. Под словом «игра» понимается совокупность правил, руководствуясь которыми игроки-участники принимают решения. Предположим, что результатом игры является плата, которую в соответствии с правилами проигравший участник платит выигравшим. Для простоты ограничимся сначала так называемыми «играми двух лиц с нулевой суммой». Для того чтобы полностью определить такую игру, нужно задать таблицу платежей – платежную матрицу, например, следующую матрицу размера 3х4:

Эта запись означает, что игрок А
выбирает одну из строк этой матрицы, а игрок В,
не зная выбора А, выбирает один из столбцов матрицы. Число на пересечении выбранных строки и столбца определяет выигрыш первого игрока (соответственно проигрыш второго). Например, если А выбрал вторую строку, а В – третий столбец, то А выиграл 5 единиц, а В их проиграл. Если же А выбрал третью строку, а В – второй столбец, то А проиграл 2 единицы, а В их выиграл.
Будем считать, что цель каждого из игроков состоит в максимизации наименьшего возможного выигрыша (соответственно минимизации наибольшего возможного проигрыша). Основной вопрос, возникающий в теории игр: существует ли наилучший способ игры у каждого из игроков, т. е. имеются ли у них оптимальные стратегии.
Прежде чем сформулировать ответ, вернемся к рассматриваемой матрице. Сразу видно, что игроку А
выгоднее всего выбрать первую строку, так как все ее элементы больше соответствующих элементов остальных строк. Точно так же игроку В выгоднее всего выбрать второй столбец, так как все элементы этого столбца меньше соответствующих элементов остальных столбцов. Следовательно, в данном примере оптимальными стратегиями будут следующие: для А – выбор первой строки, а для В – выбор второго столбца.
Число 4, стоящее на пресечении первой строки и второго столбца, носит название цены игры, т. е. платы, которую получает оптимально играющий игрок. Таким образом, в этом примере гарантированный выигрыш А – не менее 4-х единиц и гарантированный проигрыш В – не более 4-х единиц (он равен 4 единицам, если оба игрока играют оптимально).
Если оказывается, что для данной платежной матрицы минимум в какой-либо строке совпадает с максимумом в каком-либо столбце, то эти строка и столбец называются оптимальными, а их пересечение – седловой точкой
платежной матрицы. Соответствующее число и будет ценой игры.
Однако далеко не каждая матрица имеет седловую точку, например, матрица

Аналогично для В соответствующие частоты обозначим через у и (1 –у). Тогда средний выигрыш А, обозначаемый через Е (х, у), равен
Е(х,у)=4(1-х)у+х(1-у)=х+4у-5ху.
(11.17)
Нас интересует величина max min E(x,y). Имеем
x y
Еу=4-5х,
(11.18)
откуда Еу>0
при




(график на рис. 11.7). Следовательно,

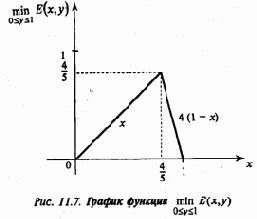
и оптимальной смешанной стратегией для А будет выбор первой строки с частотой


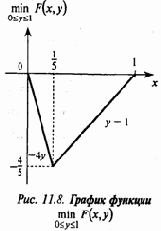
очевидно равен –Е (х, у). Нас интересует величина

F(x,y)=5xy-x-4y. (11.20)
Имеем Fx=5y-1, откуда Fx< 0 при




(график на рис. 11.8). Следовательно,

и оптимальной стратегией для А
будет выбор первого столбца с частотой


При оптимальных смешанных стратегиях выигрыш А и соответственно проигрыш В
в пять раз меньше максимально возможного при одиночной игре.
Отметим также, что в рассмотренном примере мы показали существование оптимальных стратегий и установили равенство

при этом величину Е(х,у) можно трактовать как математическое ожидание выигрыша, а величину v =

Рассмотрим теперь общий случай прямоугольной матрицы

При любой допустимой стратегии игрока A: x1 ? 0, ...,хm ? 0, x1 +x2+…+xm=1 и любой допустимой стратегии игрока В: y1 ? 0, ...,ym ? 0, y1 +y2+…+ym=1 математическое ожидание выигрыша равно

Множество допустимых стратегий x = (x1,…,xn) игрока А обозначим через X, а множество допустимых стратегий у=(у1,...,yn) игрока В обозначим через Y.
Рассмотренные выше примеры являются частными случаями общих теорем [18] для игр с прямоугольными матрицами (прямоугольными играми); из них, в частности, вытекает:
1. Величины


является ценой игры.
2. Всякая прямоугольная игра имеет цену; каждый игрок в прямоугольной игре всегда имеет оптимальную стратегию.
3. Пусть Е – математическое ожидание выигрыша в прямоугольной игре с матрицей С, имеющей цену v. Тогда для того, чтобы элемент х* =(х1*,...,х*m)Î Х был
оптимальной стратегией для игрока А,
необходимо и достаточно, чтобы для всякого j =1, 2,...,n базисного вектора y(j) =

v ? E (x*, y(j)). (11.25),
Аналогично для того чтобы элемент у*
=(y*1,...,y*n)ÎY был оптимальной стратегией для игрока В, необходимо и достаточно, чтобы для всякого элемента базисного вектора x(i) =

E (x(i), y*) ? v. (11.26)
Покажем теперь на двух примерах, как можно применить эти утверждения для вычисления цен и определения оптимальных стратегий для прямоугольных игр. В качестве таких примеров рассмотрим стратегии ловли на удочку и питания рыбы1.
1 Идея примера взята из книги Вильямса [8], которая также может служить хорошим введением в теорию игр.
Представим себе, что существование такого вида рыб, питающихся у поверхности воды, зависит от наличия трех видов летающих насекомых, которые обозначим через т1,т2
и m3
соответственно; насекомые появляются в зоне захвата с частотами 15п, 5п и п
(т. е. насекомых т2 в 5 раз больше чем m3, а насекомых т1 в 3 раза больше чем т2).
Допустим, что рыбак В
ловит рыбу А на насекомых одного из этих видов, насаживая их на крючок. Тогда матрица стратегий С ловли на удочку и питания рыб имеет следующий вид (табл. 11.1):

На основании изложенных утверждений достаточно найти неотрицательные числа х1,х2,х3, y1,y2,y3 и число, удовлетворяющее следующим условиям:
x1+x2+x3=l, y1+y2+y3=1, (11.27)
v ? -2x1, -2y1 ? v,
v ? -6x2, -6у2 ? v,
v ? -30x3, -30у3 ? v.
Заменим последние шесть неравенств на равенства. Тогда имеем
х1=у1=



(11.28)
Подставляя эти значения в равенства (11.27), получим
v =



Таким образом, цена игры для рыбы будет отрицательной и равной

Несколько усложним задачу. Предположим, что рыболов иногда использует приманку т4, которая может быть принята по ошибке за одно из трех насекомых, но которая вдвое чаще вызывает подозрение у рыб. Тогда матрица С стратегий ловли на удочку и питания рыб примет вид табл. 11.2:

Теперь достаточно найти неотрицательные числа х1,х2,х3, y1,y2,y3,y4 и число v, удовлетворяющие следующим условиям:
x1+x2+x3=l, y1+y2+y3+y4=1, (11.27)
v ? -2x1, -y4 –2y1 ? v,
v ? -6x2, -3y4 – 6у2 ? v,
v ? -30x3, -15y4 – 30у3
? v.
v ? -x1 –3x2 –15 x3
Левая система неравенства переопределена, а правая недоопределена ( в левой неизвестных больше, чем неравенств, а в правой меньше). Заметим, что если последнее неравенство в правой колонке
-15y4 –30у3 ? v. будет выполнено при у3=0, то оно будет выполнено и при всех у3>0. Следовательно, полагая у3 = 0, правую систему неравенств можно заменить системой трех линейных уравнений
-y4 –2y1 = v, -3y4 – 6у2 = v, -15y4 – 30у3 = v
с тремя неизвестными y1, у2, у4.
Ее решение, очевидно, имеет вид

Подставляя полученные выражения в равенство (11.32), где у3
=0, получим


что несколько меньше, чем в предыдущем случае. Оптимальная стратегия рыбалки имеет вид

Изучим теперь оптимальную стратегию для рыбы, так как у3, = 0, то и x3 = 0, т. е. насекомые m3
слишком опасны для жизни. Тогда из системы четырех неравенств выпадают третье и четвертое, которое при x3
= 0 является следствием двух первых (их полусуммой). Таким образом, для определения x1, х2 и v
имеем систему трех уравнений с тремя неизвестными
x1 + x2 + x3
= 1, v = -2x1, v = -6x2,
откуда

и, с учетом x3
= 0,


Значит, оптимальная стратегия для рыбы равна

цена же ее в силу (11.35) равна

Модели, основанные на теории игр, представляют собой интересный, но пока еще недостаточно изученный подход к решению стратегических экологических задач. Разработка теории для более сложных игр с ненулевой суммой и игр многих лиц, где между игроками могут создаваться коалиции, должна найти эффективное применение в экологических проектах, связанных с планированием и оценкой различных воздействий на окружающую среду.
Контрольные задания
1. Рассмотрим задачу об «оптимальном рационе» в случае трех продуктов питания (например, хлебные, молочные и мясные продукты) и трех полезных веществ (углеводы, белки, жиры). Ценовой вектор с = (с1, с2, c3) (руб.) примерно равен (10; 20; 50), а вектор b = (b1, b2, b3) минимально необходимого месячного потребления полезных веществ (кг) равен (1,2; 4; 1,5). Будем предполагать также, что матрица


Решить задачу f1(x)=

2. При тех же ограничениях решить задачу f2(x) = х2 > max .
3. Решить двухкритериальную задачу f1(x)>min, f2(x)>max, заменяя ее минимизацией суперкритерия f(x)=?f1(x)-(1-?)f2(x). Рассмотреть случаи

4. Привести геометрическую интерпретацию задач 1–3.
5. Рассмотреть задачу поиска в случае трех районов и соотношения

6. Найти оптимальную стратегию рыбака, использующего в качестве наживки мух и живца, если матрица стратегий имеет вид:

7. Найти оптимальную стратегию рыбака, если он дополнительно использует искусственных мух и блесну, а матрица стратегий в этом случае имеет вид:

